To Be Clear…
I want to be open and clear in my endeavors about moon sighting. I do not want anyone to feel any doubt or lack any certainty about the reports that I give regarding the sighting of the new moon.
Let me start by noting that I have been involved in sighting the moon since 1993, and I have gone out nearly every month since then. I have studied the moon and its motion in the sky. I am well-read on the science behind its motion and the mathematical technique employed today on predicting where the moon could be seen. Over the years, I have developed my own set of criteria as to whether or not I think the moon will be seen. I also contribute to making final decisions almost every month as to the beginning of the Islamic months with other moon sighters and committees across the United States.
Over the years, I have noticed that the following minimum parameters are needed to easily see the new moon:
Age: more than 18 hours old
Lag Time: 40 minutes or more
Elongation: 12 degrees
Altitude at Sunset: 5 degrees
Crescent Width (or Percent Illumination): 19 arc seconds or 1% illumination
The parameters for the new crescent on June 5th were as follows at the time of sunset:
Age: 27.5 hours
Lag Time: 42 minutes
Elongation: 14.8 degrees
Altitude: 6.5 degrees
Percent Illumination: 1.7%
The moon was not going to be easily seen because the lag time and the altitude at sunset were very close to the minimum values needed to see the moon easily.
Predicting the visibility of the new crescent moon has been an endeavor that dates back thousands of years. In 1997 and then updated in 1998, B.D. Yallop working for the HM Nautical Almanac Office, surveyed the methods used historically and those used in the twentieth century and developed a new criteria to predict new crescent moon visibility. if interested, Yallop’s paper can be obtained HERE. Every numerical moon prediction method used today works off of the Yallop method. Among the parameters that I mention and use above, Yallop determined that there was a mathematical functional relation between the geocentric difference in altitude between the center of the sun and the center of the moon for a given latitude and longitude on the earth, ignoring the effects of refraction, and the topocentric width of the crescent moon. In fact, Yallop found that the difference in the altitude was a cubic function of the topocentric crescent width. Let me explain some of these terms.
First, let me explain the altitude. Altitude is a measure of a celestial objects distance above the horizon as seen by an observer on the surface of the earth. There are two ways to calculate it, geocentrically and topocentrically. The geocentric calculation assumes that one is at the physical center of the sphere of the earth and the line connecting the center of the earth and the moon. This altitude is measured off of the equator of the earth. The topocentric calculation assumes one is standing on the surface of the earth and the line connecting the location on the earth and the moon does not necessarily pass through the center of the earth. The following diagram shows the two different angles.
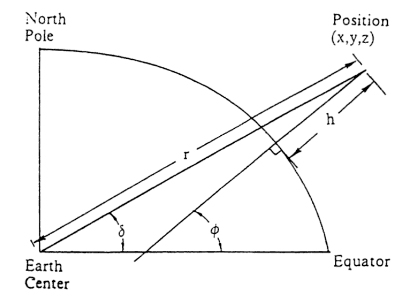
Diagram showing Geocentric and Topocentric altitude.
The angle delta, δ, indicates the Geocentric altitude and the angle phi, φ, indicates the Topocentric altitude. The topocentric altitude is of course easier to measure as one stands on the surface of the earth. The difference in the geocentric altitude between the sun and the moon requires that this quantity be measured, or calculated, for both the sun and the moon and then the difference between those two values determined. If the sun happens to be on the horizon it will have essentially a zero altitude by definition. If the moon happens to still be in the sky above the sun then the difference in the altitudes will be a positive number. If the moon had set before the sun, then the moon will be below the horizon and the difference in the altitudes would be a negative number. Thus, the difference in the altitudes is always computed at the time of sunset for any given location on the earth. The resulting number is then just the actual altitude of the moon above the horizon.
The altitude is measured in degrees and one can use a clinometer to easily measure the topocentric altitude of any celestial object, including the moon. Check here if you would like to make your own clinometer. To determine the geocentric altitude of the object one would need to employ trigonometry and some algebra, which is beyond the scope of the article at this time, but can be found by searching for it online if one desires.
Next is the topocentric crescent width. This parameter measures the width of the visible portion of the moon. The width of the moon is measured by an angle that subtends the moon as measured from earth. In the figure below it would be the angle given by W. From the earth the moon’s width measures approximately 0.5° or 30 arc minutes. It varies slightly from month to month depending on the distance between the earth and moon as the moon follows an elliptical path around the earth, sometimes a bit closer and sometimes a bit farther. The width of the crescent is of course less than the 30 arc minutes and will continuously grow from zero to a full 0.5 degrees when the moon is full. In terms of arc seconds, the moon is 1800 arc seconds wide (60 arc seconds in every arc minute). A one percent (1%) illuminated moon corresponds to a crescent width of only 18 arc seconds wide, and a 19 arc second wide moon corresponds to roughly 1.05% illumination.
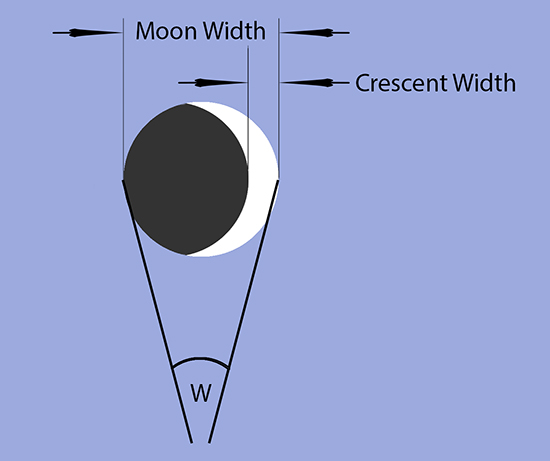
Measuring the Width of the Crescent
The crescent width is directly related to another parameter mentioned above and that is the Elongation. The elongation is also an angular measure that determines the position of the moon relative to the earth and sun. At conjunction the moon lines up with the earth and sun along what is known as the earth-moon-sun conjunction line. The diagram below shows the new moon orientation with the moon on the conjunction line, as well as showing the moon in two other positions later in its orbit around the earth. As the moon continues to move away from the conjunction line, the elongation angle continues to grow. As the moon moves along in its orbit past conjunction, the visible portion of the moon gets larger as more reflected light from the sun can bounce off and find its way down to the earth where we can view it.
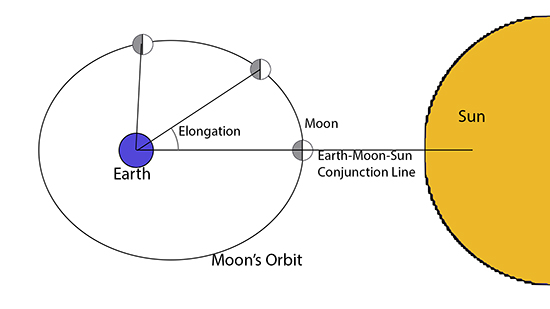
Elongation Diagram
Yallop had also discovered a mathematical functional relationship between the difference in the geocentric altitudes and the elongation and the difference in the azimuths of the moon and sun. With this other relationship Yallop was able to come up with quadratic function that related the difference in the altitudes to the difference in the azimuths of the sun and moon. So how are the probability curves generated?
Using a data set of 295 sighting reports in the past, the locations of where those sightings occurred were plotted on a map of the earth based on their latitude and longitude. Then for a given date the necessary parameters, altitudes and azimuths are computed using astronomical calculations. Given the values of the altitudes and azimuths along with the result of each individual sighting from the data set, whether the moon was seen or not seen, and whether it was seen by the unaided eye or with an optical aid, a parabolic curve is plotted on the map to fit the data as best as possible. The parabolic curve is used as it will best fit the quadratic function determined by Yallop. The technique used is called Least Squares Curve Fitting and it is a statistical method that uses pre-existing data to fit a line or other curve, such as a parabola in this case, to the data that gives the best possible fit while minimizing errors. The larger the data set used the more accurate the curve fitting becomes. Yallop initially used 295 data points and from that set determined six visibility zones; Zone A – Easily Visible to the Unaided Eye, Zone B – Visible Under Perfect Atmospheric Conditions, Zone C – Visible to the Unaided Eye After Found with Optical Aid, Zone D – Only Visible with Binoculars or Conventional Telescopes, Zone E – Not Visible with Conventional Telescopes and Zone F – Not Visible Below Danjon Limit of 7°. The Danjon Limit is the minimum elongation angle that will allow sunlight reflecting off of the moon to reach the earth. Below a 7° elongation there is not enough light reflecting off of the moon that it could be seen by any means.
Numerically the six zones are determined by the following values: Zone A – q > +0.216, Zone B – +0.216 ≥ q > -0.014, Zone C – -0.014 ≥ q > -0.16, Zone D – -0.16 ≥ q > -0.232, Zone E – -0.232 ≥ q > -0.293, Zone F – q ≥ -0.293.
Note that in moving from one zone to the next, the values of the determination parameter have common borders. Zone A and B have a common border along the 0.216 parabola line, Zone B and C along the -0.014 parabola line, Zone C and D along the -0.16 parabola line, Zone D and E along the -0.232 parabola line and finally Zone E and F along the -0.293 parabola line. Even though the above inequalities are designed to ensure any given location can be in one and only one zone, there is no margin of error between the zones and this raises many questions. What if one was standing exactly on one of the parabola lines that delineates one zone from the next? What prediction does one rely on? How far into any given zone must one move to ensure that the zone one is in will be the predictor of the probability indicated?
Again, the Yallop criteria, a statistical method using past sighting data to predict probable future sightings and the larger the data set the better the curve fit and the better the prediction of probable sighting.
The Yallop criteria for the moon on June 5th indicated that my area was in Zone C; that sighting the crescent was possible after using an optical aid to first locate the moon, however my location was very close to the border line of Zone B, crescent visible under perfect atmospheric conditions. Aside from some wispy high clouds in limited portions of the sky, we had great atmospheric conditions for sighting the moon as I had ever seen.
So what happened this past Sunday evening? Our group arrived at our viewing location, Russian Ridge Open Space Preserve along the Ridge Trail, with the following coordinates 37.3247 N 122.2087 W at an elevation of 2359 feet around 7:45 pm to 8:00 pm local PDT. We waited for the sun to set before we started to look. I knew the moon’s azimuth would be about 10 degrees to the left of the sun, approximately 1 hand span, and 6.5 degrees above the horizon, approximately 2 to 3 fingers above the horizon at the time of sunset. I directed everyone to concentrate on that location of the sky. We all looked intently.
The prime time to see the moon occurs at a time that is 4/9 of the lag time after sunset, a time determination that was also discussed by Yallop in the same above mentioned paper. At our location sunset occurred at 8:26 pm PDT. The moon set was at 9:08 pm PDT, and 4/9 of 42 minutes is 18 minutes and 20 seconds. This placed the best viewing time at 8:44 pm. Hence, as soon as it was 8:44 pm, we all started to double our searching efforts. One from the group at this time thought that he saw its lower limb poking out from the clouds that were perched right where the moon was supposed to be. Then, a few moments later, another of the onlookers thought he saw it as well. The first person though had lost sight of it. Neither could confirm with certainty. At about 8:50 pm PDT, I pull out a pair of small low power 7 x 35 binoculars (see note below), and I search the sky along the bottom edge of the clouds that obstructed our view. Within moments, I confirmed what the other two had seen with their naked eyes: the bottom limb of the moon was indeed sticking out from the clouds. I moved the binoculars from my eyes, and I could clearly distinguish that the lower limb was visible and directed others to where it was. Within 5 minutes, the moon had completely dropped out of the clouds. At this point, I was able to see it clearly and at the same time faintly. It was a very thin moon and one that was difficult to spot. However, when I directed the rest of the group to where it was in relation to clouds around it, the first two who had seen it, were able to see it once more, and they were followed by a third onlooker, then a fourth and then a fifth in addition to myself. It was then that I trained my camera on the moon and made four photos, starting at 8:58 pm. By that time the moon had dropped to about 1 or 1.5 fingers above the horizon, approximately 3 degrees above the horizon in altitude.
In all we were about 15 in number; most had a difficult time seeing it, but those of us who did see it, were certain we had seen it. We continued to watch it until just about 9:05 pm PDT when it had dropped so low that haze along the horizon was now obscuring the view.
I made the first photo of it just as it dropped out of the clouds at 8:58 pm; however, I did not set the camera controls correctly, and the moving reflex mirror in the camera caused a vibration that blurred the moon. I then made the second of four photos immediately afterwards, this time locking the mirror in place before tripping the shutter. That second photo was the photo displayed on the June 5th post. The third and fourth photos were made in the same manner however, the second photo showed the moon best. Furthermore, I have been photographing the new crescent moon with a digital camera for the last 8 years. I set the camera to photograph in RAW mode. A RAW file is not actually an image file, rather it is a file that records the CCD image sensor data as it was captured. An additional piece of software is needed to read the RAW file and covert it to an image file. In the RAW converter, I have control over the data, and I can set the exposure, brightness, contrast, highlight and shadow levels, color temperature as well as the saturation so that the image appears as best as I can recall at the time I made the photo. I cannot however, add an object that was not there, nor can I remove something that was there. Those operations can be accomplished, if so desired, in an image editing program like Photoshop. When the RAW file is opened in the converter it is very dull and with very low contrast and, in most cases, looks nothing like the actual scene. This is by design to ensure the darkest part of the image and the lightest part of the image contains actual detail. Pure black and pure white in a digital image contain no details at all. The four photos shown below are the four that I made on the evening of June 5th, without any adjustments made to the RAW files other than opening the files in the converter and then saving them as JPEG files for displaying on the web.
Note on Binoculars: I have not used binoculars to search for the new moon since September of 2003. On that particular occasion, I was able to see the moon with a pair of 10×50 binoculars, but I could not see it with my naked eyes. I had a group with me at that time as well, and they could not see the crescent even with the binoculars. It put me in a difficult position, as according to the Shari’ah, the sighting obligated me to start the new month but not so for any others. I was instructed by one of my teachers to stop using optical aids in searching for the new moon. Hence, this past Sunday night, on June 5th, was the first time I had used binoculars in thirteen years. My children have grown up with moon sighting, and while they were all to young to understand the use of binoculars thirteen years ago, they grew up with hearing about that incident 13 years ago and have been with me consistently over this time. Three of my four children are all considered adults now under Shari’ah and these three were all among the five besides myself that saw the crescent on June 5th. As I pulled the binoculars out, they all urged me to put them away. They all said, “Don’t cheat!”
Earlier that evening I was in contact with other colleagues that I work with in determining how to respond to other sighting claims from the United States and abroad. Positive sighting reports had come in from Peru and Chile but did not include the details that would have allowed us to evaluate the sightings. I was fairly certain that we would get reports from either Arizona or South Texas based on the Yallop probability curves for those areas, and sure enough, we did get a report from Frisco Texas. I personally interviewed the man who made that report, and it sounded like a valid report. He was not alone but had his wife and his adult daughter with him, and all three saw it. Furthermore, he did indicate to me that there were others in his area that had seen it as well. In discussing this report with my colleagues, we had decided to declare a positive sighting had been made but that we would wait until after sunset PDT to make the final call once we had a chance to search for the moon. I was already convinced that the month had started, and thus my “cheat” was more of a self edification than anything else. Once I established its location with the binoculars, I was able to direct others to seeing it, and once I pulled the binoculars from own eyes, the moon was there, faint, but clearly there, seen with my naked eyes, just as the Yallop curves had indicated. The other naked eye sightings were just that – naked eye sightings, as they did not use the binoculars, something the Yallop curves did not indicate.
Finally going back to my criteria based on my sighting experience. The moon of June 5th at the location of our observation met all the criteria indicating that we should have been able to see the moon. Since the lag time was very close to the minimum of 40 minutes and that the altitude of the moon was very close to the minimum of 5 degrees needed, it was going to be a difficult moon to see. Indeed it was a very difficult moon to see. However, had we not had clouds to contend with that covered the portion of the sky at 8:44 pm where the moon should have been, we might have seen it earlier while it was at its optimum contrast. The first of the sighters who did think he saw the lower limb but then later lost it, did think he saw it at just about the time of optimum viewing of 8:44 pm.
I would like people to understand that I would not have made the claim of seeing the moon if we did not actually see it with our naked eyes. The responsibility of making such a claim when it is not true carries a great burden; in fact, any time I make a claim to have seen the moon, a great burden comes along with it. I do not take moon sighting lightly. The worship of billions of Muslims sometimes rides on my sightings, and I am very careful with it.
I hope this post settles any questions anyone might have had with the sighting that we made on June 5th. I ask that you all keep me and my team of moon sighters in your prayers and pray that we can continue to keep this Sunnah of our Prophet Muhammad (peace and blessings upon him) alive and well and that we can once again re-establish it as the dominant method of determining our religious months and holidays.
Until next time, Peace to All and Ramadan Mubarak!



















